Still an ongoing project for discrete hyperparameter tuning of an Artificial Neural Network (ANN) with Bayesian Optimization (BO), where the number of nodes and number of input and output samples are being optimized for prediction and simulation error.
Why this project?
This project is purely for educational purposes and to learn how to use BO for discrete hyperparameters. The ANN will consist of 1 hidden layer and a varying amount of nodes to be optimized.
Background
Using machine learning techniques date as far back as 1943, but implementations were often put aside due to lack of computational power. Nowadays, this computational power has been drastically increasing and therefore things are suddenly much more accessible than before. The idea with this project is to perform data-driven modeling of an actuated pendulum also called the “Unbalanced disk”. More information about the setup and the datasets used you can check out @GerbenBeintema. The dynamics of the pendulum will be encapsulated by an Artificial Neural Network (ANN) that optimizes its neurons such that it can predict and simulate how the pendulum behaves. Designing such an ANN comes with a lot of guessing and hand tuning what the amount of hidden layers and the amount of neurons should be. This project is about trying to give an educated guess what the optimal amount of nodes are for an ANN with 1 hidden layer. Bayesian Optimization (BO) will be used to optimize the amount of nodes. This optimization technique uses Gaussian Processes (GP), because they are able to track uncertainties, which you need to be able to guess good query points based upon the exploration/exploitation trade-off. The benefit of using BO instead of for example Grid Search is that you need less trials to get to the same or even better result. The problem is that normal bayesian optimization relies on your hyperparameters to be continuous (which is normally a good thing), but for hyperparameters that are discrete in nature like the number of nodes or hidden layers of an ANN it is much more challenging.
Goal
Show that by using discrete BO on #nodes and #input and output samples yield better results within 1 hour of optimizing on a GTX 1080 GPU than using random search. This all will be done with a standard ANN with 1 hidden layer.
NARX model
A Nonlinear Autoregressive Exogenous (NARX) model is used to describe the dynamics of the system.
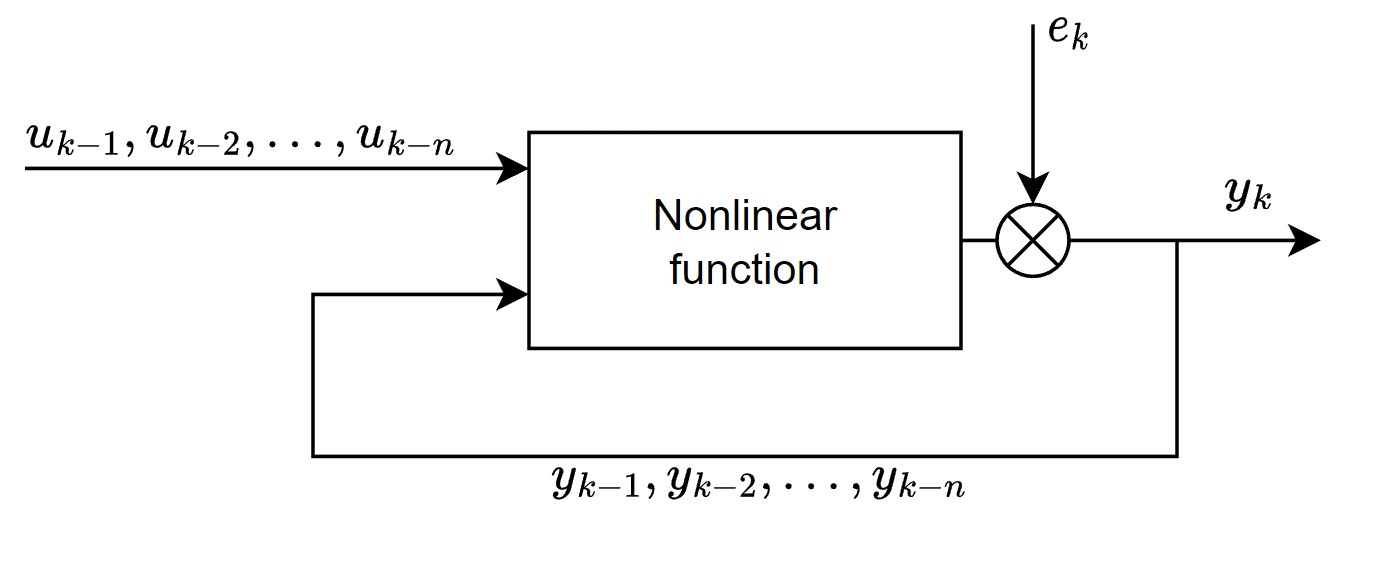
Where $y_k$ is the output of the model and $u_k$ is the input. The e_k term is the white-noise that influences $y_k$ and therefore also all its past values. The amount of past inputs that are taken into account are denoted by $n_b$ and the amount of past outputs that are taken into account to determine the current output are denoted by $n_a$. Both $n_a$ and $n_b$ are considered hyperparameters, because the amount of information needed to accurately describe the dynamics are both system and data dependent.
Artificial neural network structure
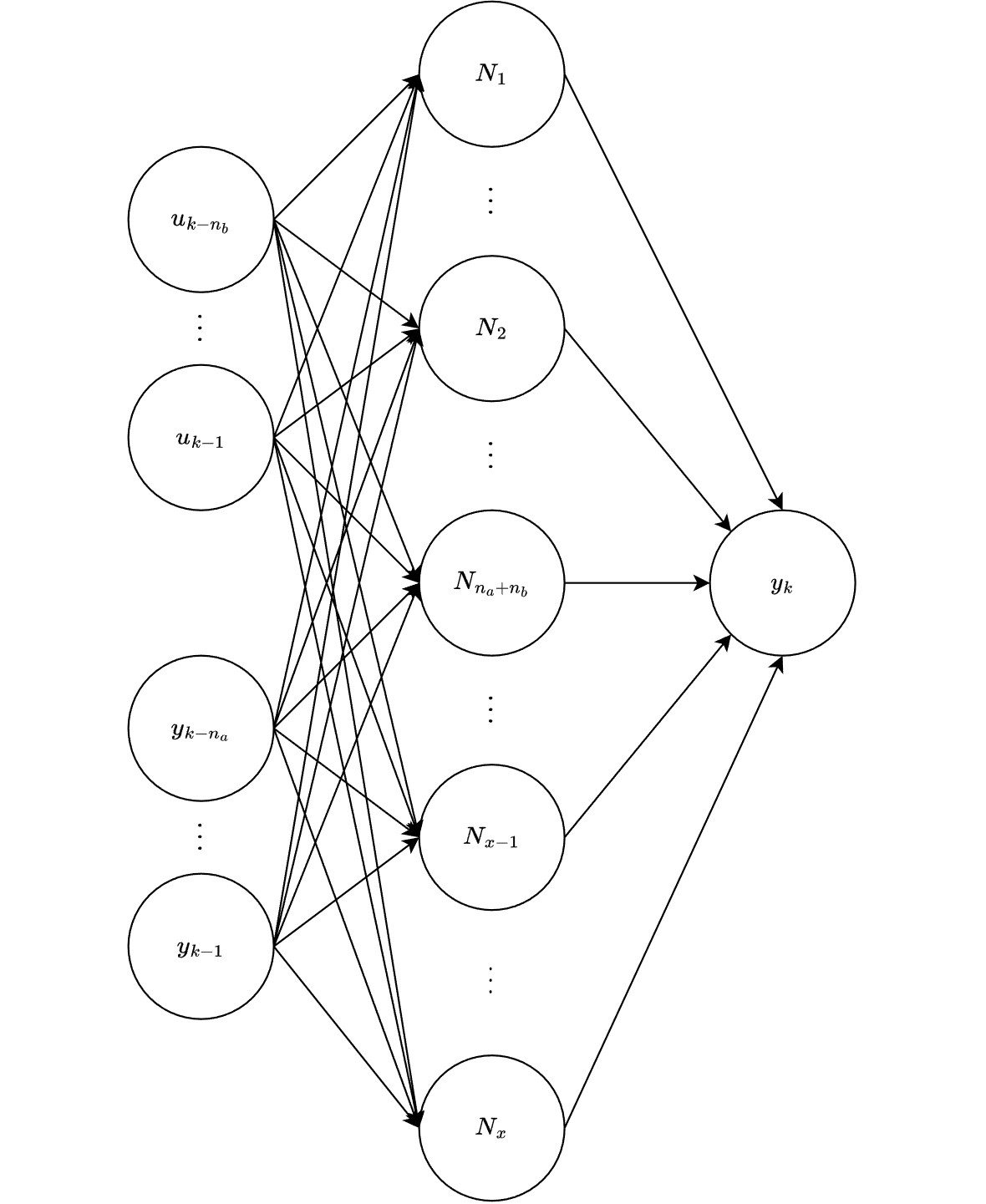
Prediction and simulation
Coming soon
Implementation
Currently the different libraries, bayes_opt , botorch and Ax are experimented with and checked for suitability for discrete hyperparameter tuning.
Hyper parameters
Work in progress
Acquisition function
Work in progress
Kernel selection
Work in progress
Activation function selection
Work in progress